PID制御とは、P(比例), I(積分),D(微分)を用いた制御手法である。では、典型的な問題、バネマスダンパ系を用いて実装してみよう。以下の図にバネマスダンパ系の図を示す。マスの質量を \( m \) [kg] ,バネ定数を\(k\)[N/m],ダンパ係数を\(c\)[Ns/m]とし、マスに\(F\)[N]の力がかかっているとする。以下のバネマスダンパ系の運動方程式は
$$m\ddot x=F-kx-c\dot x$$
となる。
では、上式にPID制御を用いて、力\(F\)[N]を制御し、目標値に変位を制御してみよう。目標値を定数u[m]とすると
$$F=P(u-x)+I\int (u-x)dt+D\frac{d(u-x)}{dt}$$
となる。ここで、P,I,Dはそれぞれ比例ゲイン、積分ゲイン、微分ゲインである。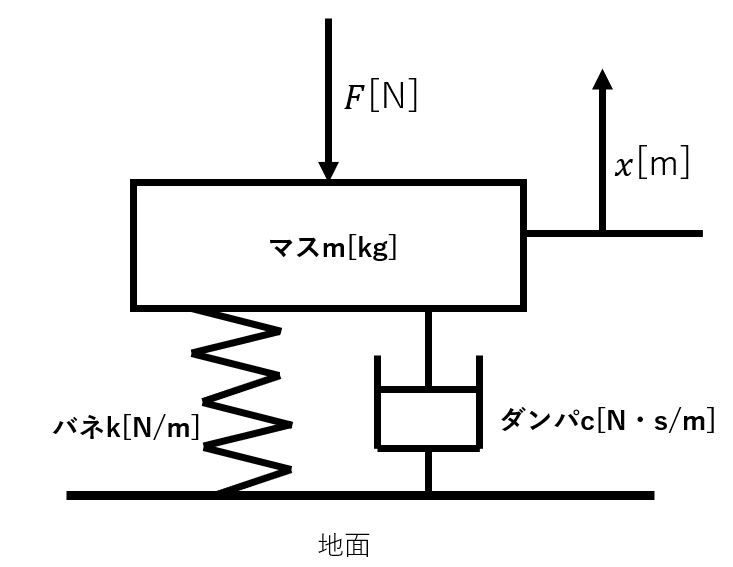
運動方程式、PID制御則を立式できたので、これを用いてバネますダンパ系を制御シミュレーションをしてみよう。
シミュレーションはmathworks社が販売しているMATLAB/Simulinkを用いる。以下の図に作成したsimulinkモデルを示す。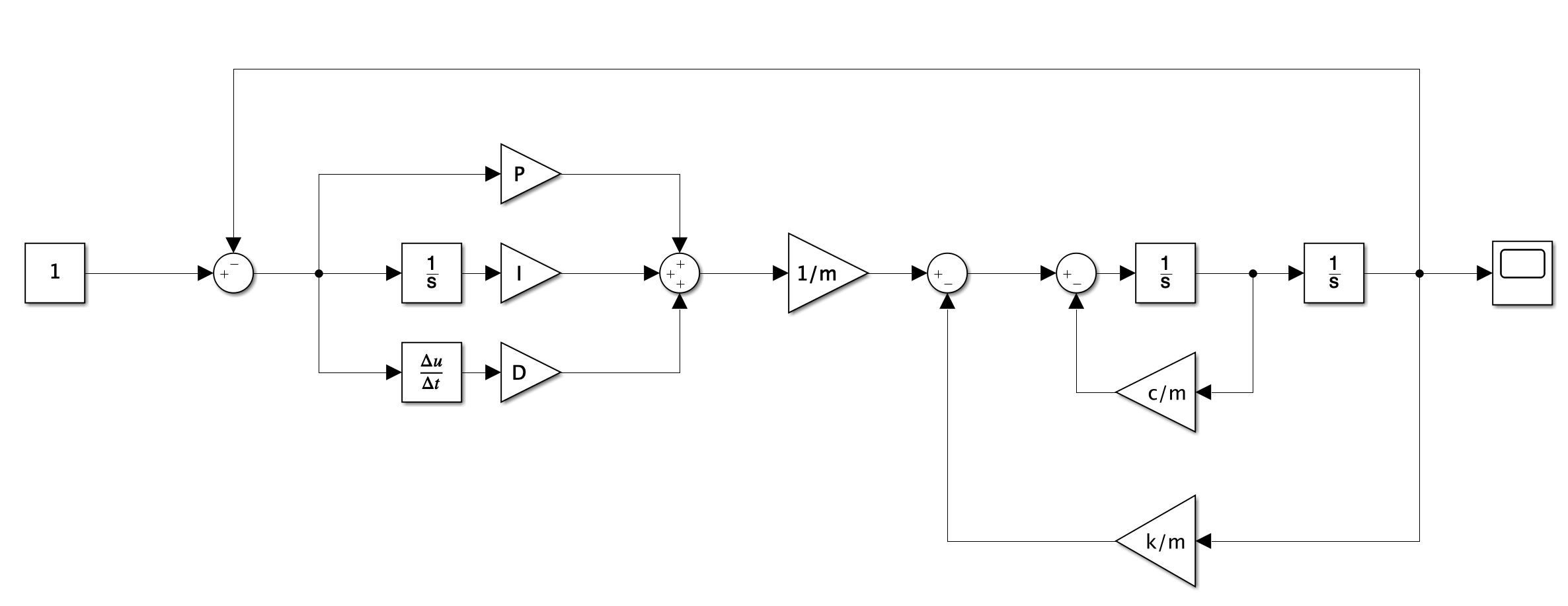
simulinkブロックからわかるように入力は1となっている。P,I,Dおよびm,k,cの値は全て1とした所、シミュレーション結果は以下の図のようになった。図を見るとわかるようにバネマスダンパ系の出力は目標値1に追従していることがわかる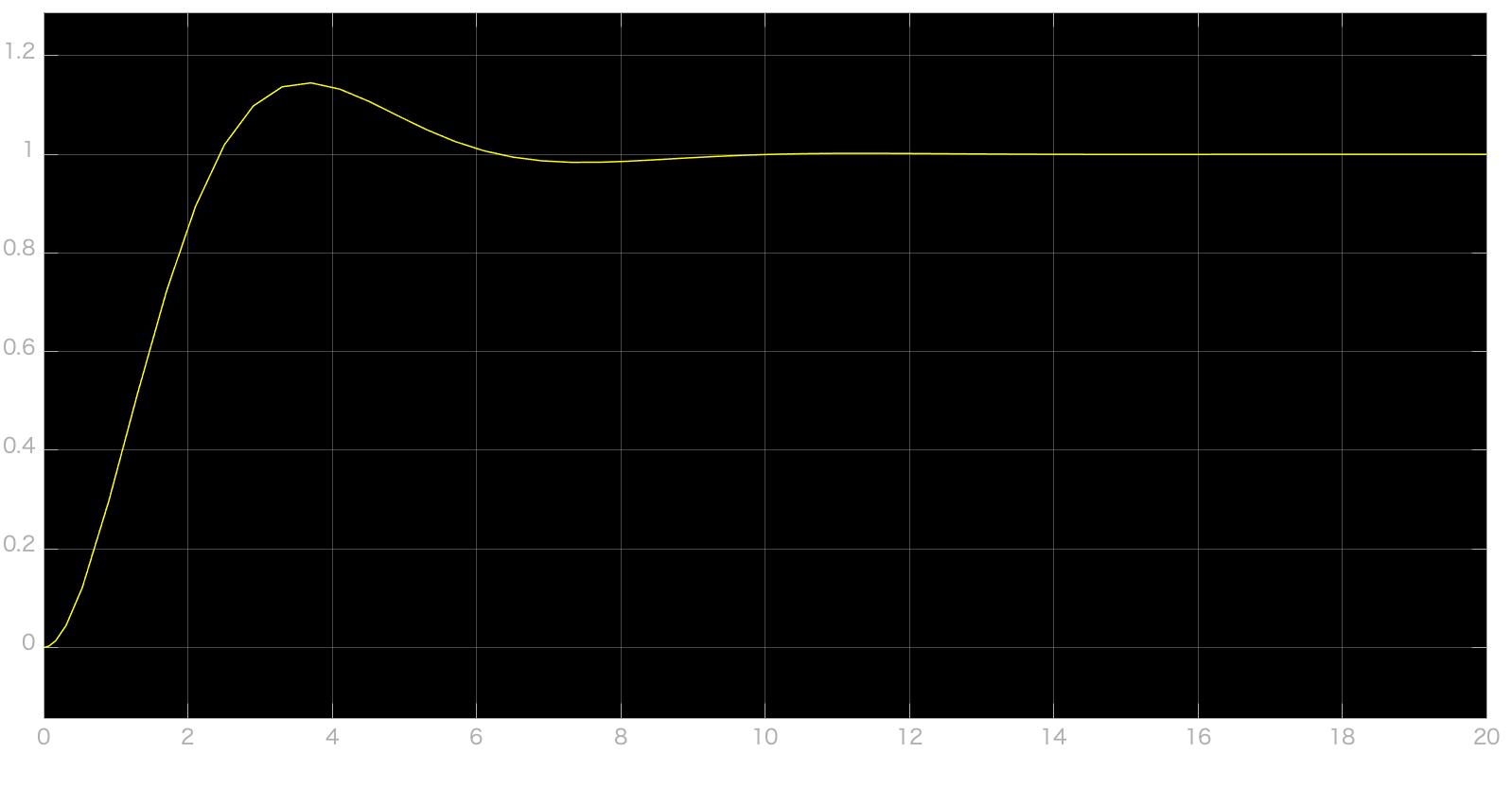
カテゴリー: 未分類
自動車の運動学モデル
自動車の速度を \( v \) [m/s],旋回角度を\(\theta\)[rad],ステアリング角度を\(\delta\)[rad]とすると、自動車の運動学モデルは
$$\dot x=v\cos\theta\\
\dot y=v\sin\theta\\
\dot\theta= \frac{v }{L}\tan\delta$$
となる。